Please, how can one change the pitch standard from A=440Hz to any other value?

In that case I need a little more info:
1) Open your Finale document, and take a look in the MIDI/Audio menu, the two top items in the MIDI/Audio menu.
Which one is selected? - Is it {Play Finale Through MIDI} ?
2) You tell that you use Mac Finale, and that you sometimes “need to use Finale on friend's Windows”.
Does that mean the very same Finale document, sometimes on your Mac Finale, and sometimes on friend’s Windows?
Ok, I am a Finale pro user since 1998, so I will appreciate your general explanation on all options Finale gives me. (This is the first time I am required to change the default pitch). I can use either MIDI or Audio Units on my Mac.
About the Windows version, I need general instructions, not specifically for the same finale document. I could not find the answer on the manual, sorry.
This is an oldie. I've not tried it but found this from 2009.
As you know, the playback software defaults to a tuning of A=440 Hz.
Hence you have to do a workaround to adjust the pitches.
1) Changing the tuning is easier with Play Finale Through MIDI.
It works the same way on Windows and Mac.
It is done with the Expression Tool.
You create a new expression with playback effect Pitch Wheel.
It takes some calculation to find the exact Pitch Wheel value.
As you probably know, the interval of an octave means a doubling of the frequency, e. g. from 440Hz to 880Hz.
The interval of a chromatic half step means a frequency ratio of {the 12th root of 2} = ca. 1.059463…
The interval from 440Hz to 442Hz means a frequency ratio of 442/440 = 1.004545…
Since we hear interval sizes on a logarithmic scale, we need to compare the logarithms of the frequency ratios.
Hence the size of a chromatic half step can be measured as 1/12 of the logarithm of 2.
For playback it is convenient to set the size of 1 chromatic half step to 1 “Interval Unit”.
This is done by dividing the {frequency ratio}’s logarithm by {1/12 of the logarithm of 2}.
Thus we get that
- 1 chromatic half step = 1 “Interval Unit”
- an octave (frequency doubling!) = 12 “Interval Units”
- the frequency ratio 442/440 = 0.078514… “Interval Units”
When setting the Pitch Wheel value it makes a difference whether you are using Human Playback or not.
With Human Playback off 1 chromatic half step = 4096 Pitch Wheel units
To turn up the tuning from 440Hz to 442Hz, set the Pitch Wheel value to
4096 * 0.078514 = 322
With Human Playback on an octave equals 8192 Pitch Wheel units.
This means that 1 chromatic half step = 682.6666…
To turn up the tuning from 440Hz to 442Hz, set the Pitch Wheel value to
682.6666 * 0.078514 = 54
Phew!
Do you “get it” this far?

Zoltan,
If you want to change the tuning of all your instruments and you are using the ARIA Player as your playback device, you can also change the tuning within the player itself. The Settings page in the ARIA Player has the option to set the tuning of all the instruments in the player to a pitch standard from 380 to 451.
https://usermanuals.garritan.com/ARIAPlayer/Content/tuning.htm
Thank you Peter Thomsen,
Your explanation on the units is very helpful. It works fine now.
I've noticed that, with "audio units" instead of MIDI, the Pitch Wheel units behaviour is quite different. Please, can you explain the difference?
Thanks to David Cusick about the ARIA settings: I will use and forward this information as well.
… I've noticed that, with "audio units" instead of MIDI, the Pitch Wheel units behaviour is quite different. Please, can you explain the difference? …
2) Changing the tuning is another story with {Play Finale Through Audio Units}.
It is confusing that with Audio Units it does not matter, whether Human Playback is On or Off.
In playback through Audio Units an octave always equals 8192 Pitch Wheel units - even with Human Playback Off.
Side note:
{Play Finale Through MIDI} works the same way in Windows Finale and Mac Finale.
On The Other Hand, the two Finale platform versions are different in playback of sampled sounds.
Mac Finale uses Audio Units while Windows Finale uses VST.
This means that you have to Reassign Playback Sounds when opening the same document on the other platform.
But you probably knew that already.
Peter Thomsen,
"When setting the Pitch Wheel value it makes a difference whether you are using Human Playback or not.
With Human Playback off 1 chromatic half step = 4096 Pitch Wheel units
To turn up the tuning from 440Hz to 442Hz, set the Pitch Wheel value to
4096 * 0.078514 = 322
With Human Playback on an octave equals 8192 Pitch Wheel units.
This means that 1 chromatic half step = 682.6666…
To turn up the tuning from 440Hz to 442Hz, set the Pitch Wheel value to
682.6666 * 0.078514 = 54"
I tried this (but I had to enter a value of -540 to lower the pitch to A=415, not 54)
The pitch changed as required, BUT
The first note (in a manual intro bar of ⅛ introducing 4/4) is anticipated by a quarter note value (approximately) on the first repeat (but not the second repeat)
I just tried the expression on a piece where the time signature is straight 3/4 with no shortened intro bar, and the first note is still anticipated by approximately one quarter note on all instruments.
It is possible that this is caused by a clash between Human Playback and NotePerformer, I suppose ...

Regards,
Robert Thomson
Robert Thomson,
I am not sure I understand.
1) What version of Finale? - perhaps v27.2?
2) Windows Finale or Mac Finale?
3) You quote a passage where I am talking about
- Play Finale Through MIDI,
- Human Playback on.
* I suppose that this is what you are doing, too, - right?
4) To get a tuning of A = 415 Hz you need to lower the tuning by a little more than a chromatic half-step.
Are you sure that a Pitch Wheel value of -540 lowers the tuning to A = 415 Hz?
I could be wrong here, but it seems to me that the correct Pitch Wheel value is -691.
Still assuming the settings I mentioned in 3) above.
5) Your description of the problem is a bit unclear to me:
“The first note (in a manual intro bar of ⅛ introducing 4/4) is anticipated by a quarter note value (approximately) on the first repeat (but not the second repeat)”.
Is this what you hear on the first repeat?

Regards,
Peter Thomsen
Hi Peter,
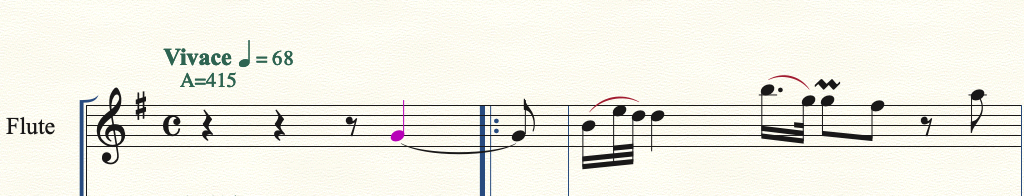
Please sign in to leave a comment.
14 comments
Date Votes